نوشته های مشابه

روانگرايی خاکهای ماسـه ای و رسـی و ماسه رسی در برابر وقوع زمين لرزه

آبان ۲۵, ۱۴۰۲

اثر عوامل زمین شناسی که برای حفر تونل باید در نظر بگیریم

آبان ۶, ۱۴۰۲

فرایند بتن پاشي (شاتكريت) برای تونل بلافاصله پس از انجام عمليات حفاري

شهریور ۳۱, ۱۴۰۲

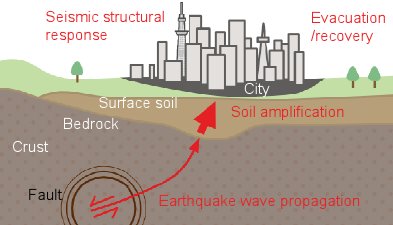
اثرات ساختگاهی برکلیه خصوصیات مهم زلزله شامل دامنه ، محتوای فرکانسی و مدت دوام ، اثر قابل ملاحظه ای می­گذارد.به عبارتی خصوصیات زلزله با توجه به مشخصات فیزیکی و دینامیکی ساختگاه می­تواند در فرکانس­های مشخصی تشدید یا تضعیف گردد. میزان تاثیرگذاری خواص مواد لایه­های زیر سطحی ، توپوگرافی ساختگاه و خصوصیات حرکت ورودی می باشد. [۳]

در واقع امواج زلزله در هنگام انتشار از سنگ بستر به سطح زمین تحت تاثیر خصوصیات دینامیکی آبرفت در فرکانس های خاص تقویت و یا تضعیف می­شود که درصورت برابری این فرکانس با فرکانس طبیعی سازه پدیده تشدید رخ می دهد که باعث خرابی سازه میشود. لایه های رسوبی در سطح زمین به طور قابل ملاحظه ای حرکات زمین لرزه را تقویت می­کند که این پدیده به نام اثرات ساختگاهی مطرح است. جنبش نیرومند زمین می تواند حتی در فاصله ای بسیار اندک تغییراتی زیادی داشته باشد.[۳]

روش های مختلفی برای تعیین اثرات ساختگاهی به کارگرفته شده است که برای مطالعات ریز پهنه­ بندی و همچنین جهت بررسی خطر زمین لرزه برای سازه های خاص به کار گرفته می شوند. این اثر نخستین بار در سال ۱۹۵۷ در زمین لرزه سان فرانسیسکو توسط سید و ادریس[۱](۱۹۷۲) مورد توجه قرار گرفت. مطالعات این محققین دلالت بر اهمیت اثرات خاک بر محتوای فرکانسی حرکات توانمند زمین و بیشینه شتاب آن داشت. مشخصات سیستم خاک با استفاده از سیگنال های ثبت شده، در حوزه زمان و فرکانس قابل بررسی است. [۴]

[۱] Seed, Idriss

– بررسی روش ها :

برای دریافت متن کامل به ایمیل [email protected] پیام دهید

در تجزیه و تحلیل خطر لرزه ای، اثرات منبع زلزله، مسیر انتشار و شرایط محلی محل بر لرزش های زمین باید به درستی در نظر گرفته شود. در رویکردهای تجربی رایج، ما اغلب اثرات ساختگاهی را با استفاده از یک پارامتر یا ترکیبی از پارامترها مشخص می کنیم و سپس از پارامتر(های) ساختگاه به عنوان متغیر(های) پیش بینی کننده پیوسته یا گسسته (از طریق طبقه بندی) برای برآورد پاسخ های ساختگاه استفاده می کنیم. ، سرعت موج برشی میانگین زمانی در ۳۰ متر بالای یک ستون ساختگاه[۵] ، به طور گسترده ای به عنوان یک پروکسی پذیرفته شده است. [۲۳]

برای تجزیه و تحلیل خطر لرزه ای در مقیاس منطقه ای، استفاده از ،  در مدل سازی های حرکت زمینی، شناسایی آن را در مکان هایی که اندازه گیری های ، خاص ساختگاه در دسترس نیست، ضروری می کند. برای پرداختن به این موضوع، رویکردهای استنباط مختلفی پیشنهاد شده است که ،  را با سایر

ویژگی‌های زمینی که به راحتی به دست می‌آیند، اغلب پراکسی‌های توپوگرافی و/یا زمین‌شناسی مرتبط می‌کنند. [۲۳]

یک رویکرد برای گرفتن اثرات ساختگاهی، استفاده از مدل های پیش بینی کلی است که تقویت ها را به متغیرهای پیش بینی کننده مختلف مرتبط می کند. متغیرهای پیش‌بینی‌کننده می‌توانند موارد زیر باشند: [۲۳]

(الف) پارامترهای مکان از اندازه‌گیری‌های ژئوتکنیکی/ژئوفیزیکی درجا، به عنوان مثال، میانگین سرعت موج برشی در بالاترین سطح ۳۰ متر ( )، ضخامت رسوبات، و فرکانس تشدید محل.

(ب) نمونه هایی از مدل ها یا نقشه های منطقه ای موجود، به عنوان مثال، شیب توپوگرافی، زمین، و زمین شناسی.

همچنین، با توجه به ماهیت اثرات ساختگاه وابسته به فرکانس، هیچ پراکسی ساختگاهی نمی تواند به خوبی تقویت را در همه فرکانس ها توصیف کند. بنابراین، در چند سال گذشته مطالعات بسیاری در جستجوی یک نشانگر ساختگاه جایگزین یا مکمل برای ، به عنوان مثال، پارامتر عمق و فرکانس تشدید ساختگاه (به عنوان مثال، ژو[۱]و همکاران، (۲۰۲۰ b) ؛ هاشاش[۲] و همکاران، (۲۰۲۰)؛ حسنی[۳] و اتکینسون، (۲۰۱۸)؛ غفرانی و اتکینسون[۴]، (۲۰۱۴)؛ پیتیلاکیس[۵] و همکاران، (۲۰۱۳)).

[۱] Zhu

[۲] Hashash

[۳] Hassani , Atkinson

[۴] Ghofrani , Atkinson

[۵] Pitilakis

مدل‌های گروه اول اغلب در مدل‌های اخیر حرکت زمینی تعبیه شده‌اند GMM[1] در حالی که مدل‌های دسته دوم در طرح پاسخ ساختگاه منطقه‌ای یا جهانی اعمال می‌شوند. هنگام در نظر گرفتن این مدل ها، باید پوشش فضایی و دقت را بالانس کرد. علاوه بر این، پاسخ‌های ساختگاه در مکان‌های خاص را می‌توان با استفاده از تحلیل پاسخ زمینی یک بعدی (۱D) یا روش ریشه مربع امپدانس (SRI[2]) تخمین زد (جدول ۱-۱). GRA[3] پاسخ‌های ساختگاه را با مدل‌سازی انتشار امواج صفحه عمودی  در لایه‌های رسوبی طبقه‌بندی‌شده افقی ارزیابی می‌کند. در مقابل، SRI بر اساس تئوری پرتو است و فقط از سرعت‌ها و چگالی‌های یک چهارم طول موج متناظر با فرکانس استفاده می‌کند. هر دو روش به یک مدل مکان دقیق نیاز دارند و GRA همچنین به خواص غیرخطی خاک برای آنالیزهای خطی یا غیرخطی معادل نیاز دارد. [۲۳]

[۱] ground-motion models

[۲] square-root-impedance

[۳] ground response analysis

یکی دیگر از تکنیک های خاص ساختگاه ، اصلاح تجربی نسبت طیف فوریه مولفه افقی به مولفه عمودی، یعنی نسبت طیفی افقی به عمودی است (HVSR[1]). در این مطالعه HVSR به عنوان روش “c-HVSR” نشان می­دهیم. بر اساس نظریه فیلد پراکنده ، آن را به عنوان یک رویکرد تجربی در نظر گرفتند و عملکرد آن را در مقایسه با GRA با استفاده از جفت‌های رکورد های سطح-پایین ارزیابی کرد. c-HVSR به هیچ مدل ساختگاهی نیاز ندارد اما نیاز به رکورد در محل و توابع تصحیح از پیش تعریف شده برای منطقه مورد مطالعه دارد. [۲۳]

با استفاده از این تکنیک‌های تخمین (GRA، SRI، c-HVSR و مدل‌های پاسخ ساختگاه کلی) چقدر می‌توانیم اثرات ساختگاه را تاکنون پیش‌بینی­کنیم؟ پرداختن به این سوال برای شناسایی بهترین رویکرد فعلی و سپس اتخاذ و تکرار بهترین روش بسیار مهم است. اما برای مقایسه تکنیک های مختلف چند مانع وجود دارد. اولاً، ما به اندازه گیری های پاسخ ساختگاه قابل اعتمادی نیاز داریم که بتوان از آنها به عنوان داده‌های «معیار»، «استاندارد طلایی» یا «زمین واقعی» برای ارزیابی یا کالیبره کردن سایر رویکردها/مدل‌های برآورد استفاده کرد. علاوه بر این، ما به ابرداده های دقیق ساختگاه (مانند مدل های ساختگاه یک بعدی و ثبت زمین لرزه ای) نیاز داریم تا همه این رویکردها را در مکان های جداگانه آزمایش کنیم. [۲۳]

[۱] horizontal-to-vertical spectral ratio

با این حال، چنین ارزیابی جامع و قوی را می توان به لطف حجم زیادی از داده های حرکت زمینی انباشته شده در شبکه های متراکم حرکت قوی، کی- نت[۱] وکیک- نت[۲] ، در ژاپن، با اطلاعات دقیق ساختگاه ، محقق کرد. بنابراین، یک مجموعه داده پاسخ ساختگاهی قابل اعتماد از رکوردها برای تعداد زیادی از ساختگاه از طریق تکنیک وارونگی کلی ، مدل‌سازی تجربی حرکت زمین (ترم ساختگاه δS2Ss[3]، لویکنس[۴] و همکاران، ۲۰۲۱) ایجاد می‌شود. نسبت طیفی سطح به گمانه عمیق (SBSR[5]، ژو و همکاران، ۲۰۲۰) (جدول ۱-۱) آورده شده است. [۲۳]

[۱] K-NET

[۲] KiK-net

[۳] Site term from analyses to GMM residuals

[۴] Loviknes

[۵] Surface-to-borehole spectral ratio

جدول ۱-۱٫ تکنیک های مختلف برای تعیین کمیت پاسخ های ساختگاه محل زلزله.[۲۳]

 

ابزار	مرجع	پیش نیاز	شرح	رویکرد
اندازه­گیری	رخنمون سنگ	ثبت همزمان در هدف و محل رخنمون  سنگ و نزدیک آن (بدون اثرات ساختگاه)	نسبت طیفی استاندارد	SSR
اندازه­گیری	سنگ در عمق	ثبت همزمان در جفت گمانه به هم پیوسته	نسبت طیفی سطح به گمانه	SBSR
اندازه­گیری	یک ساختگاه یا مجموعه ای از ساختگاه ها	ایستگاه‌های متعدد ثبت شده از چندین رویداد که GMM انتخاب‌شده برای آنها قابل استفاده است	اصطلاح ساختگاه از تجزیه و تحلیل تا باقیمانده های GMM	δS2S
اندازه­گیری	یک ساختگاه یا مجموعه ای از ساختگاه ها	ایستگاه های متعدد با ثبت چندین رویداد	تکنیک وارونگی کلی	GIT
مدل سازی عددی	رخنمون سنگی یا سنگ درعمق	مدل ساختگاه یک بعدی (پروفیل های چگالی، سرعت و میرایی، کاهش مدول و منحنی های میرایی)	تجزیه و تحلیل پاسخ زمین	GRA
تحلیل تقریبی	رخنمون سنگی	مدل ساختگاه یک بعدی (پروفیل های چگالی و سرعت، پارامتر تضعیف)	ریشه مربع امپدانس	SRI
پیش بینی تجربی	رخنمون سنگی یا سنگ درعمق	توابع تصحیح عمودی (و پارامترهای ساختگاه) و تابع HVSR	تصیح افقی به عمودی	c-HVSR
پیش بینی تجربی	رخنمون سنگی	پارامترهای ساختگاه	مدل های پاسخ ساختگاه کلی	Amp

– روش ریشه مربع امپدانس (SRI)

[۱] square-root-impedance

روش ریشه مربع امپدانس (SRI) یک روش سریع برای محاسبه تقویت تقریبی ساختگاه است که به جزئیات مدل‌های سرعت بستگی ندارد. روش SRI پاسخ پیک مدل‌هایی با کنتراست امپدانس بزرگ در نزدیکی پایه‌شان را دست‌کم می‌گیرد، اما تقویت‌های آن مدل‌ها اغلب نزدیک یا برابر با ریشه میانگین مربع پاسخ رزونانس کامل نظری (FR[1]) مودهای بالاتر است. از سوی دیگر، برای مدل‌های سرعتی که از گرادیان‌ها تشکیل شده‌اند، بدون تغییر امپدانس قابل‌توجه در محدوده‌های کوچک عمق، روش SRI به طور سیستماتیک پاسخ FR نظری را در یک محدوده فرکانس وسیع دست‌کم می‌گیرد. برای مدل‌های گرادیان که معمولاً برای ساختگاه های سنگی کلی استفاده می‌شود، روش SRI پاسخ FR را حدود ۲۰ تا ۳۰ درصد دست کم می‌گیرد. با وجود دست کم گرفتن مداوم تقویت‌ها از محاسبات نظری FR، با این حال، تقویت‌های روش SRI اغلب ممکن است تخمین‌های مفیدتری از تقویت‌ها نسبت به روش FR ارائه دهند، زیرا تقویت‌های SRI به جزئیات مدل‌ها حساس نیستند و پیک‌های زیادی را نشان نمی‌دهند. فقدان حساسیت به جزئیات مدل‌های سرعت، روش SRI را در مقایسه پاسخ مدل‌های سرعت مختلف، علی‌رغم هرگونه دست کم‌گرفتن سیستماتیک پاسخ، مفید می‌سازد. سرعت متوسط ​​یک چهارم طول موج، که برای روش SRI اساسی است، به خودی خود در خصوصیات ساختگاه مفید است و به این ترتیب، پارامتر اساسی مورد استفاده برای توصیف پاسخ ساختگاه در تعدادی از معادلات پیش‌بینی حرکت زمین اخیر است. [۶]

تئوری پرتو پیش‌بینی می‌کند که دامنه حرکت در امتداد یک مسیر پرتو با ریشه دوم امپدانس زمین لرزه ای ساختگاه Z که  نسبت معکوس دارد، با  و  به ترتیب چگالی و سرعت انتشار موج زمین لرزه ای مشاهده کرد که پاسخ در سطح یک لایه ثابت منفرد نسبت به حرکت سطحی نیم فضا ایجاد شده با حذف لایه مشابه نسبت ریشه دوم امپدانس‌های لرزه‌ای نیم‌فضا و لایه­ است.[۷] این ایده را به چند روش مهم میتوان گسترش داد.

[۱] full resonant

گاهی اوقات به عنوان روش یک چهارم طول موج (QWL) نیز شناخته می شود، اما ترجیح داده میشود  از عبارت SRI برای قسمت تقویت ساختگاه ازاین روش استفاده شود که از سرعت و چگالی QWL استفاده می کند. [۶]

توجه داشته باشید که جوینرو همکاران (۱۹۸۱) تقویت ساختگاه را با استفاده از روش SRI تخمین زدند، اما در مقاله بعدی، جوینرو فومال[۱](۱۹۸۴، ۱۹۸۵)  از محاسبات QWL برای به دست آوردن سرعت های متوسط برای مکان هایی که حرکات قوی را ثبت کرده بودند استفاده کردند و از این سرعت ها برای توصیف هر مکان در منطقه استفاده کردند. توسعه معادلات پیش بینی حرکت زمین (GMPEs). جوینر و فومال از معادله (۲-۱) مستقیماً در تحلیل خود استفاده نکردند. [۸]

در یک برنامه مشابه، به جای عمق متناسب با پریود مورد نظر، از سرعت متوسط ۳۰ متر به عنوان متغیر مکان استفاده کرد، زیرا سرعت های موج برشی اندازه گیری شده در آن عمق برای بیش از نیمی از رکوردهای مورد استفاده در تجزیه و تحلیل آنها در دسترس بود. [۹]

تقویت  در معادله (۲-۱) را می توان به عنوان دامنه در امتداد مسیر پرتو در نظر گرفت، که بر روی صفحه ای نشان دهنده سطح آزاد، نسبت به حرکت روی صفحه افقی در عمق مرجع، نمایش داده می­شود. تقویت‌های محاسبه‌شده از معادله (۲-۱) در شبیه‌سازی‌های مدل تصادفی که در آن حرکات در سطح زمین محاسبه می‌شوند، با شروع از منبع استفاده شده‌اند. [۱۰]

در چنین کاربردهایی یک عامل اضافی که نشان دهنده اثر سطح آزاد است (معمولاً ضریب ۲، زیرا امواج سطح SH فرض می شود) باید اعمال شود. تقویت  را همچنین می توان به عنوان نسبت حرکت در سطح آزاد نسبت به حرکت در سطح یک نیمه فضا در نظر گرفت که با برداشتن تمام مواد بالاتر از عمق مرجع ایجاد می شود، با این فرض که اثر سطح آزاد همان، به طوری که آن را از نسبت کنسل می شود. گسترده­ترین استفاده از روش SRI احتمالاً در تعیین توابع تقویت پوسته مورد استفاده در شبیه سازی حرکات زمین است. [۱۱]

مدل‌های سرعت مورد استفاده در این برنامه‌ها عموماً با گرادیان مشخص می‌شوند، بدون تضاد امپدانس قابل توجهی، تقویت های SRI به طور مداوم تقویت های FR برای چنین مدل هایی را در طیف گسترده ای از فرکانس ها دست کم می گیرند. دست کم گرفتن آنچنان نیست ، با این حال، حداکثر حدود ۳۰٪ است. علاوه بر این، مشخص نیست که روش FR ،که امواج سطحی را فرض می‌کند، باید برای محاسبه تقویت از عمق منبع زمین لرزه‌هایی که حرکت زمین برای آنها شبیه‌سازی شده است، به سطح استفاده شود. روش SRI در تخمین تقویت‌های پوسته مورد استفاده در محاسبات رو به جلو حرکات زمین مفید است. این امر به‌ویژه زمانی صادق است که تقویت‌های پوسته از روش SRI برای استنباط ویژگی‌های منبع، مانند پارامتر گشتاور لرزه‌ای و پارامتر تنش، از رکورد ‌ها استفاده می‌شوند، و این ویژگی‌ها سپس در محاسبات رو به جلو حرکت زمین (با استفاده از همه مدل‌های مشابه) استفاده می‌شوند. پارامترهای مورد استفاده در وارونگی داده ها. این یک فرآیند ثابت است که در آن هرگونه سوگیری سیستماتیک در تقویت‌های پوسته در فرآیندهای معکوس و رو به جلو جبران می‌شود، تا زمانی که فرکانس‌های مورد استفاده در وارونگی مشابه فرکانس‌های پیش‌بینی‌های رو به جلو باشد. [۶]

استفاده دیگر از روش SRI در مقایسه تقویت‌ها برای مدل‌های سرعت مختلف است. در تعدادی از مطالعات، مدل‌های سرعت توسط محققین مختلف در یک مکان یا در مکان‌های نزدیک به‌دست آمده‌اند. روش سنتی مقایسه این مدل‌ها نشان دادن نمودارهای سرعت در مقابل عمق است، اما این روش نسبت به نمایش تقویت‌های حرکت زمین برای مدل‌های مختلف مفیدتر است. همانطور که به طور کلی در عمل مهم است. مشکل استفاده از محاسبات FR  برای محاسبات تقویت این است که گسسته سازی مدل ها می تواند منجر به پیک ها و فرورفتگی های ظاهری در پاسخ شود که از یک مدل متفاوت است به دیگری، و سپس نسبت‌های پاسخ می‌توانند به شدت در نوسان باشند ، تغییرات اساسی نسبت را با فرکانس پنهان می‌کند. البته، میانگین‌های تقویت‌های FR بر فرکانس را می‌توان قبل از تشکیل نسبت‌ها استفاده کرد، اما SRI همان کار را ساده‌تر انجام می‌دهد. مزیت دیگر تقویت‌های SRI این است که نسبت تقویت‌ها بالاتر از یک فرکانس کاملاً مشخص به ساختار سرعت زیر عمق کوچک‌تر به پایین دو مدل سرعتی که مقایسه می‌شوند وابسته نیست. این بر خلاف محاسبات FR است، که برای آن صرفاً جایگزین کردن ماده زیر حداکثر عمق مدل‌های سرعت با یک نیمه فاصله سرعت ثابت می‌تواند نتایج گمراه‌کننده‌ای ایجاد کند، مگر اینکه تغییر واقعی در امپدانس‌ها در پایین مدل یا وجود داشته باشد. سرعت برای محدوده قابل توجهی از اعماق زیر پایین مدل اساساً ثابت است (بنابراین تقریباً یک نیم فاصله). روش SRI مزایای زیادی در محاسبه تقویت‌های هموار و تقریبی ساختگاه برای طیف گسترده‌ای از مدل‌های سرعت دارد. این روش سریع است، به جزئیات مدل سرعت بستگی ندارد، فرکانس تقویت را با هر عمق مرتبط می‌کند، و بسیاری از قله‌ها و فرورفتگی‌ها را که معمولاً در محاسبات نظری FR مشاهده می‌شوند، صاف می‌کند. (این پیک ها و فرورفتگی ها اغلب در پاسخ های متوسط ساختگاه محاسبه شده از داده های واقعی دیده نمی شوند).از سوی دیگر، روشSRI به طور مداوم پیک ها را در سیستم های تشدید دست کم می گیرد، و پاسخ مدل های گرادیان را بدون تضاد امپدانس قابل توجه در یک محدوده فرکانس وسیع دست کم می گیرد. با این حال، برای دو مدل گرادیان مورد استفاده برای توسعه تقویت‌های پوسته‌ای که معمولاً در شبیه‌سازی‌های حرکت زمینی روش تصادفی به کار می‌روند، کمتر برآورد حداکثر حدود ۳۰ درصد است که با عدم قطعیت در تعدادی از پارامترهای مورد استفاده در شبیه‌سازی‌ها قابل مقایسه است و بسیار زیاد است که کوچکتر از عدم قطعیت های معمولی در حرکات زمین مشاهده شده است. [۶]

– روش نسبت طیفی افقی به عمودی (HVSR)

یک روش برای به دست آوردن فرکانس تشدید ساختگاه ، رویکرد نسبت طیفی افقی به عمودی (HVSR) است. این تکنیک پس از یک سری مقالات توسط ناکامورا[۳] (۱۹۸۹) [۱۳]که اخیراً چند سوء تفاهم را در مورد به اصطلاح “روش ناکامورا” روشن کرده است، شتاب بیشتری گرفت. [۱۴] از آن زمان، تحقیقات بیشماری در مورد اجرای روش HVSR بر روی نوفه های محیط یا زمین لرزه، همانطور که توسط باراد[۴] (۱۹۹۵) بررسی شد، شروع شد. [۱۲]

برای تعیین فرکانس تشدید یک مکان معین با استفاده از روش های نسبت طیفی (به عنوان مثال، HVSR) بر روی داده های زلزله، می توان از شکل موج کامل (از رسیدن  تا انتهای ) یا جزئی (معمولاً پنجره موج S) با نسبت سیگنال به نویز بالاتر از یک سطح خاص استفاده کرد. سپس باید نسبت‌های طیفی را بر روی PSA [5]صاف شده یا FAS [6]هر رکورد محاسبه کرد و سپس نسبت‌های طیفی به‌طور میانگین در تمام رکوردها در محل را بدست آورد. در مرحله بعد، از منحنی نسبت طیفی متوسط، می‌توان تمام قله‌های مهم ( ) را مشخص کرد که اغلب به‌عنوان نقاط ماکزیمم محلی با وضوح مشخص (مثلاً بزرگ‌تر از ۲٫۰) ویا معیارهای پایداری تعریف می‌شوند. [۱۵] سپس از این قله های مهم، می توان فرکانس اولین پیک ( ) یا فرکانس بالاترین پیک ( ) را به عنوان فرکانس تشدید ساختگاه انتخاب کرد. [۱۲]

میرایی مورد استفاده در محاسبه طیف پاسخ (به عنوان مثال، ۵٪) یک اثر هموارسازی اتفاقی دارد. با این حال، اگر از  برای محاسبه نسبت‌های طیفی استفاده شود، قبل از تقسیم مولفه افقی بر همتای عمودی آن، هموارسازی بیشتری نسبت به  لازم است. انتخاب روش‌های هموارسازی (به عنوان مثال، نوع عملگر هموارسازی و درجه هموارسازی) بر مقدار نسبت طیفی و متعاقباً تعیین کیفیت پیک‌های قابل توجه تأثیر می‌گذارد. از این رو، هموارسازی ناهمگن همچنین می تواند باعث عدم تطابق در فرکانس تشدید شود. علاوه بر این، در تمام این مطالعات ، فرکانس تشدید ساختگاه از پیک های قابل توجه شناسایی می شود، اما آنچه که یک پیک قابل توجه را واجد شرایط می کند، به طور ذهنی تعریف می شود. تعریف پیک های قابل توجه از مطالعه ای به مطالعه دیگر متفاوت است. همچنین، پس از تشخیص تمام پیک های قابل توجه در یک منحنی نسبت طیفی متوسط، فرکانس پیک اول ( ) یا بالاترین ( ) به عنوان فرکانس تشدید ساختگاه در نظر گرفته می شود. برخی از مطالعات [۱۶] از  استفاده کردند در حالی که برخی دیگر [۱۶]   را انتخاب کردند. اغلب فقدان یک توجیه مبتنی بر شواهد برای انتخاب یکی به جای دیگری وجود دارد، که همچنین مسئول ناسازگاری در فرکانس تشدید ساختگاه است. [۱۲]

مراحل اصلی تعیین فرکانس ساختگاه با استفاده از تکنیک  به شرح زیر است:

• محاسبه وهر سری زمانی (شکل موج کامل).
• صاف کردن و با استفاده از پنجره کونو و اوماچی[۷] (۱۹۹۸)

به دست آوردن  با تقسیم میانگین هندسی دو جزء افقی (NS و EW) یک رکورد خاص بر مؤلفه عمودی آن (V):

[۱] Fumal

[۲] horizontal-to-vertical spectral ratio

[۳] Nakamura

[۴] Bard

[۵] pseudo-spectral acceleration

[۶] Fourier amplitude spectrum

[۷] Konno, Ohmachi

 

– تکنیک وارونگی تعمیم یافته (GIT)

۱-۳-۱-۲- تجزیه و تحلیل بر اساس تکنیک وارونگی طیفی

این روش GIT بر اساس زمین‌لرزه  هوکایدو تابو[۲](۲۰۱۸) و زلزله منطقه  اوزاکای شمالی در سال ۲۰۱۸ توسط ناکانو[۳] و همکاران در سال(۲۰۱۹) انجام شد. [۱۹]

[۱] General inversion technique

[۲] Hokkaido ,Tobu

[۳] Nakano

در اینجا، برای دامنه طیف فوریه در بخش موج  شکل موج‌های لرزه‌ای، از فرمول‌  با استفاده از تقریب میدان دور موج  استفاده شده .

– روش تجزیه و تحلیل پاسخ زمین GRA

[۱] Ground Response Analysis

در رویکرد غیرخطی GRA، نیمرخ خاک با استفاده از مدل پارامتری جرم  چند درجه آزادی به سیستم جرم  -فنر – میراگر تبدیل می‌شود. معادله دینامیکی حرکت (معادله ۲-۱۲) در هر مرحله زمانی با استفاده از یکپارچه سازی عددی برای تجزیه و تحلیل پاسخ خاک حل می شود. تکنیک ادغام عددی مانند روش نیومارک β (نیومارک[۱] ۱۹۵۹) ممکن است استفاده شود. [۲۱]

هر مدل تنش-کرنش غیرخطی، با پیروی از معیارهای Masing یا غیر Masing، در طول فرآیند ادغام استفاده می شود. در ابتدای هر مرحله زمانی، رابطه تنش-کرنش برای به دست آوردن خواص خاک مورد استفاده در آن مرحله زمانی ارجاع می شود. کاهش سختی خاک با تعداد سیکل های بارگذاری که بر اساس تولید فشار آب منفذی مدل شده است، می تواند به دقت در این روش محاسبه شود. [۲۰]

[۱] Newmark

سختی (منحنی کاهش مدول) و نسبت میرایی برای لایه‌های مختلف خاک با استفاده از فرمول‌های ژنگ و ایشیباشی[۱] (۱۹۹۳) مدل‌سازی شده‌اند. این فرمول‌بندی‌ها دارای ویژگی‌های خاک مانند فشار محدود، نسبت تحکیم بیش از حد، شاخص پلاستیسیته، زاویه اصطکاک داخلی هستند.[۲۰] سپس کاهش مدول و منحنی‌های میرایی با استفاده از روش MRDF برازش می‌شوند تا پارامترهای مدل تنش-کرنش غیرخطی را تعریف کنند. میرایی ویسکوز کرنش کوچک مستقل از فرکانس در نظر گرفته شده است (فیلیپس و هاشاش ۲۰۰۹). [۲۲]

در مطالعه دودیپ بوسا[۲] وهمکاران ۲۰۱۷جنبش قوی زمین لرزه سیکیم [۳](۲۰۱۱) در نزدیکی منطقه آگارتالا، با ماکسیمم شتاب از سطح سنگ بستربزرگای  (PBRA[4]) 0.02g  و سه مولفه کوچک شده جنبش  با PBRA 0.04g ، ۰٫۰۸g و ۰٫۱۸g ثبت شد، به عنوان ورودی برای تحلیل حاضر استفاده شده است.[۲۰] طبق­آیین نامه  IS: 1893-I (2002)، ضریب منطقه (Z) برای آگارتالا ۰٫۳۶g تعریف شده است. حداکثر شتاب زمینی ممکن را بر اساس حداکثر خطر لرزه ای احساس شده نشان می دهد. زمین لرزه پایه طراحی (DBE[5]) برای آگارتالا را می توان ۰٫۱۸g به دست آورد، یعنی DBE = Z/2 (IS: 1893-I 2002).

[۱] Ishibashi , Zhang

[۲] Devdeep

[۳] Sikkim earthquake

[۴] peak bedrock level acceleration

[۵] design basis earthquake

بنابراین، مقدار ۰٫۱۸g (PBRA) به عنوان یک مقدار محدود کننده برای افزایش مقیاس اجزای جنبش قوی زمین انتخاب شده است. این حرکات در پایه نیمرخ خاک اعمال شده است. پروفیل خاک برای چهار مولفه حرکت زلزله سیکیم با PBRA مختلف تجزیه و تحلیل می شود. پاسخ خاک در معرض این حرکات ورودی، در قالب پروفایل های PHA[1]، ضریب تقویت (AF)[2]، کرنش برشی و طیف پاسخ ارائه می شود. پس از آن، در مطالعه دودیپ بوسا وهمکاران (۲۰۱۷) حساسیت روانگرایی رسوب خاک نیز تعیین می شود. [۲۰]

[۱] peak horizontal acceleraton

[۲] amplification factor

برای دریافت متن کامل به ایمیل [email protected] پیام دهید

هزینه ۱۰۰ هزار تومان